6 января 2024 /
0 комментариев
/
25 просмотров
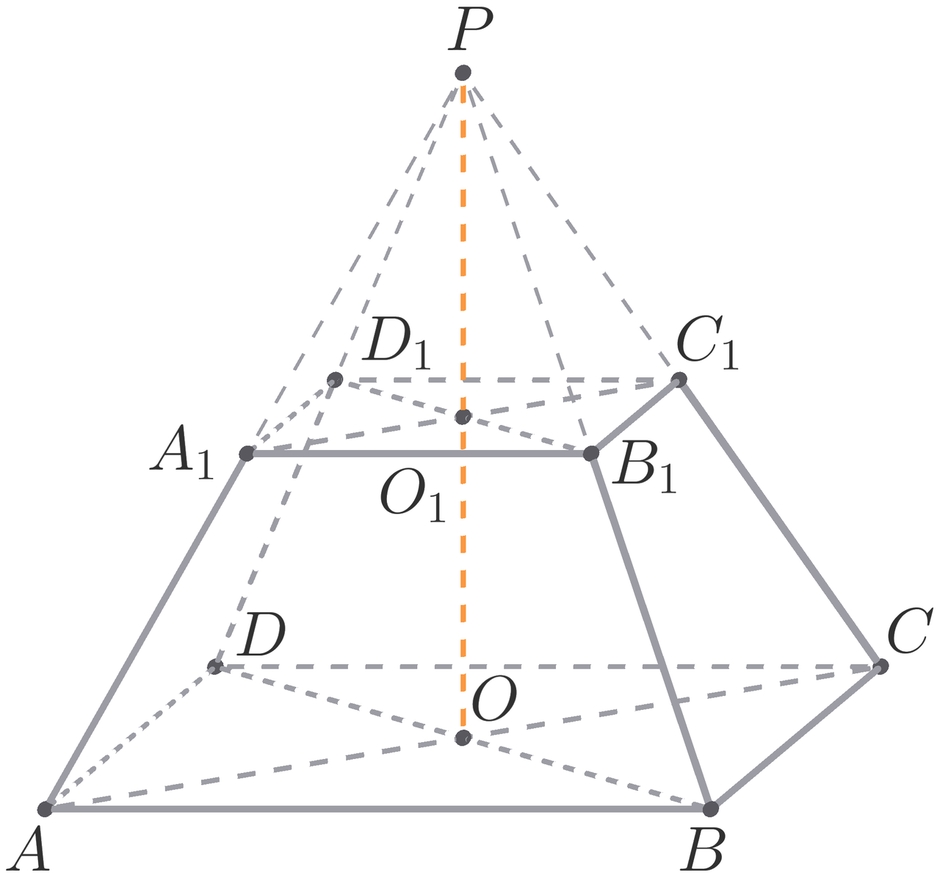
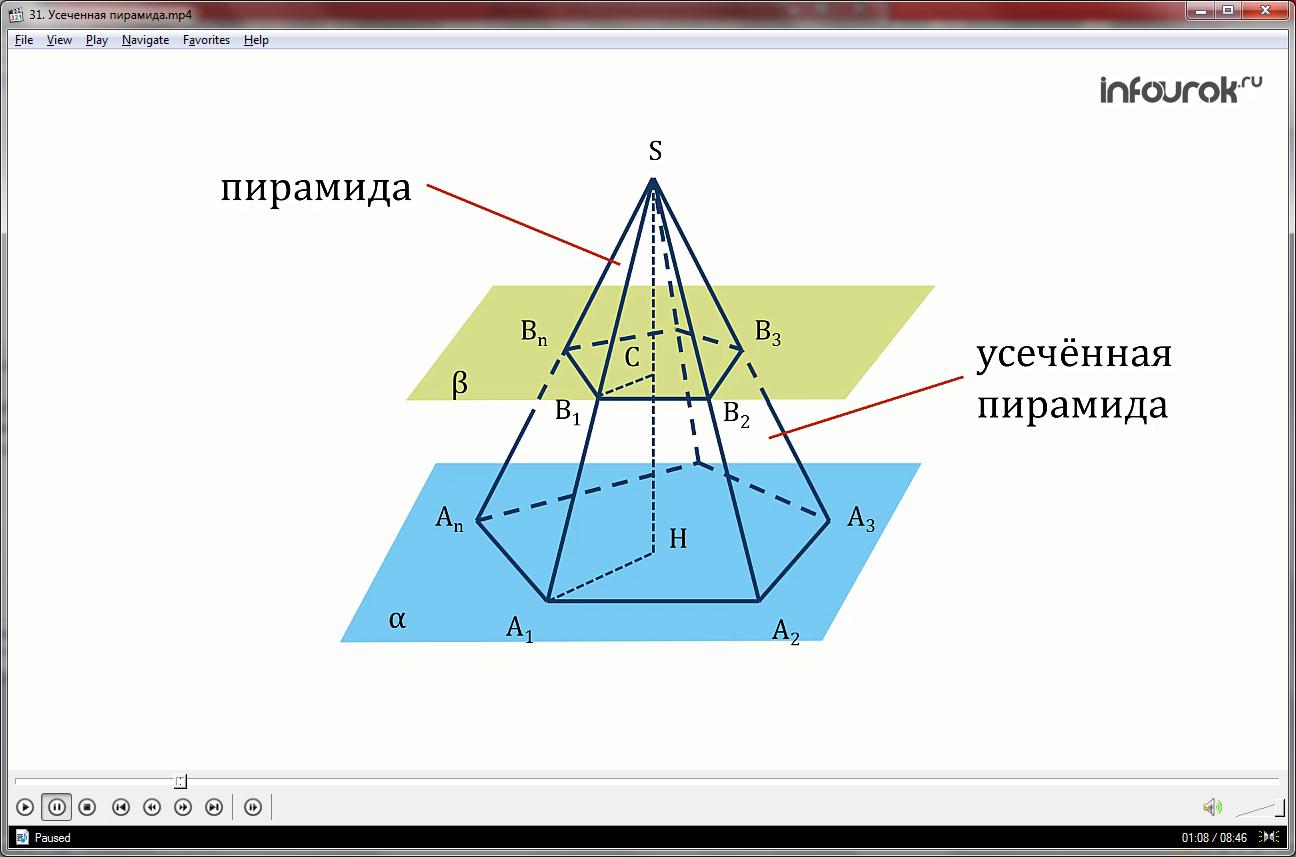
Треугольная усеченная пирамида - это геометрическое тело, получаемое путем усечения треугольной пирамиды параллельно ее основанию. Она имеет особые математические и геометрические свойства, которые делают её интересным объектом изучения.

1
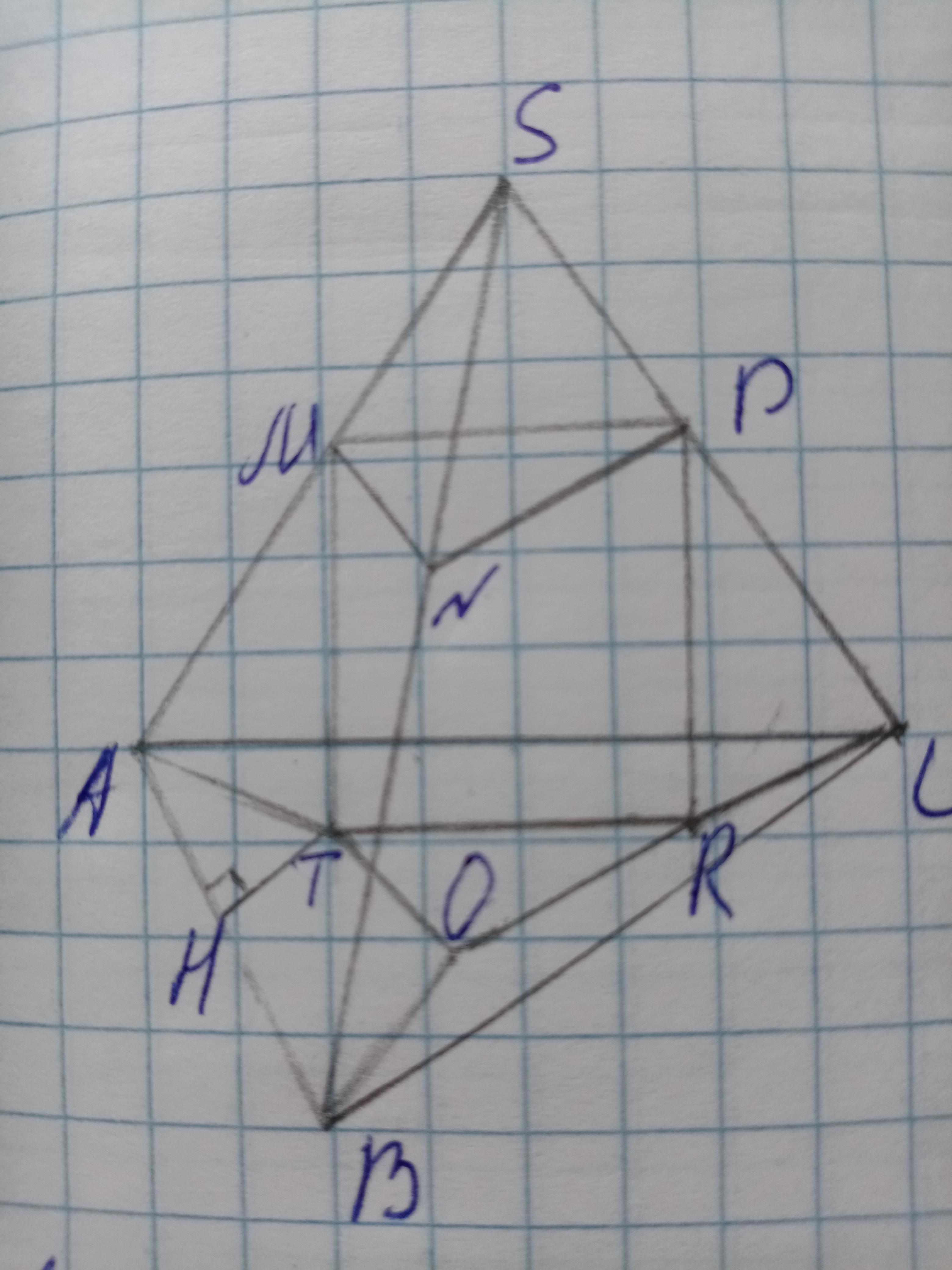
2
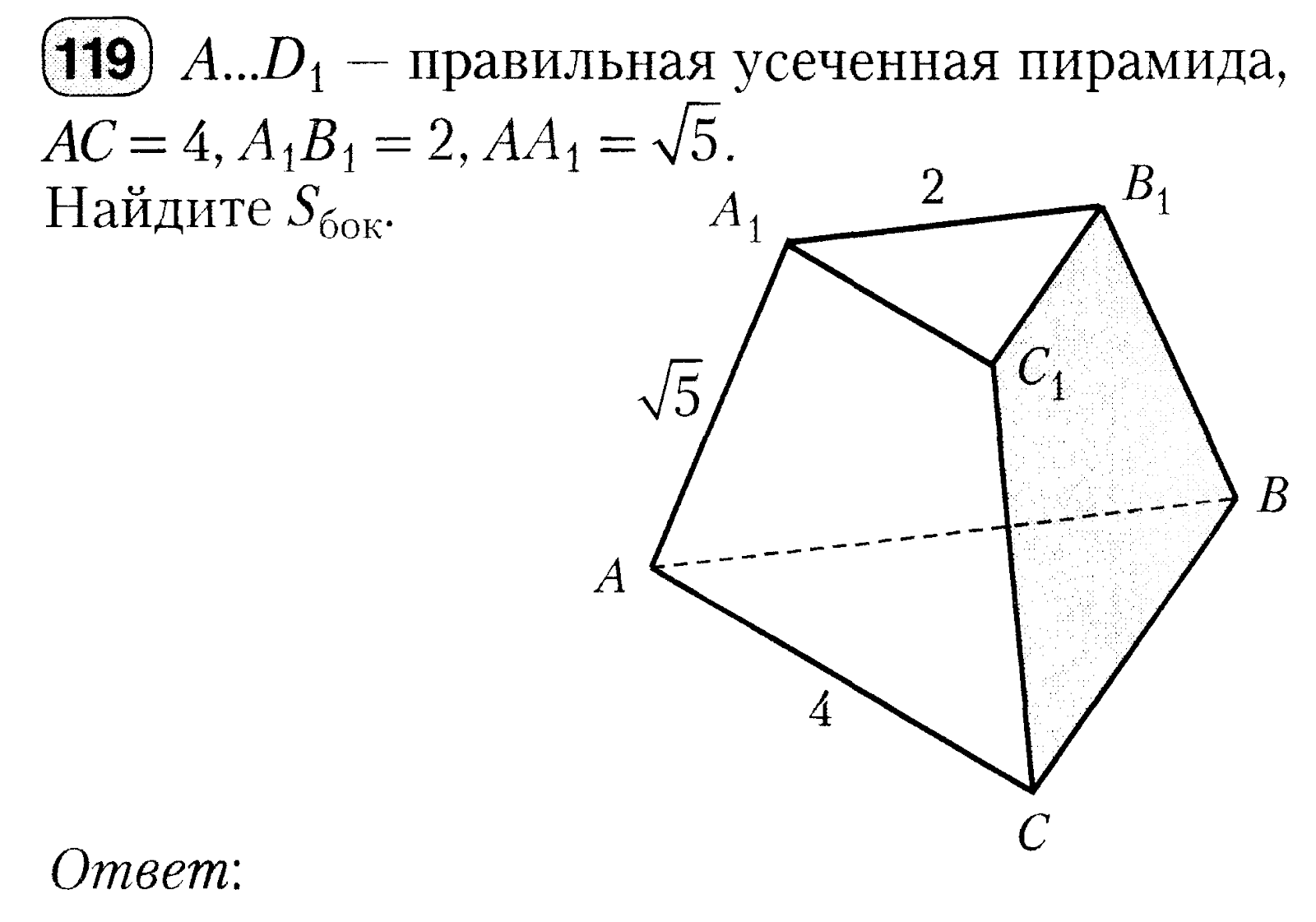
3
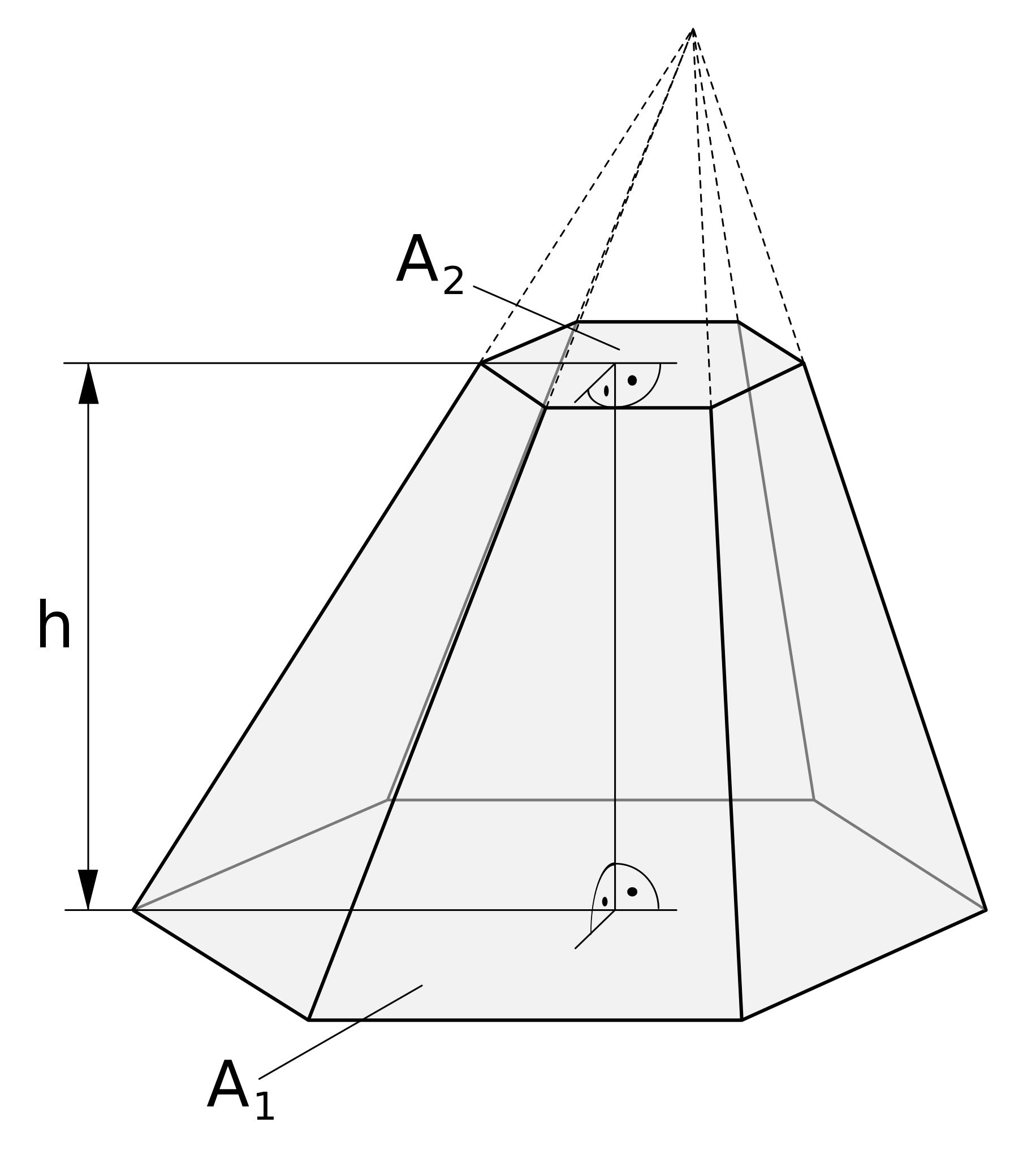
4

5
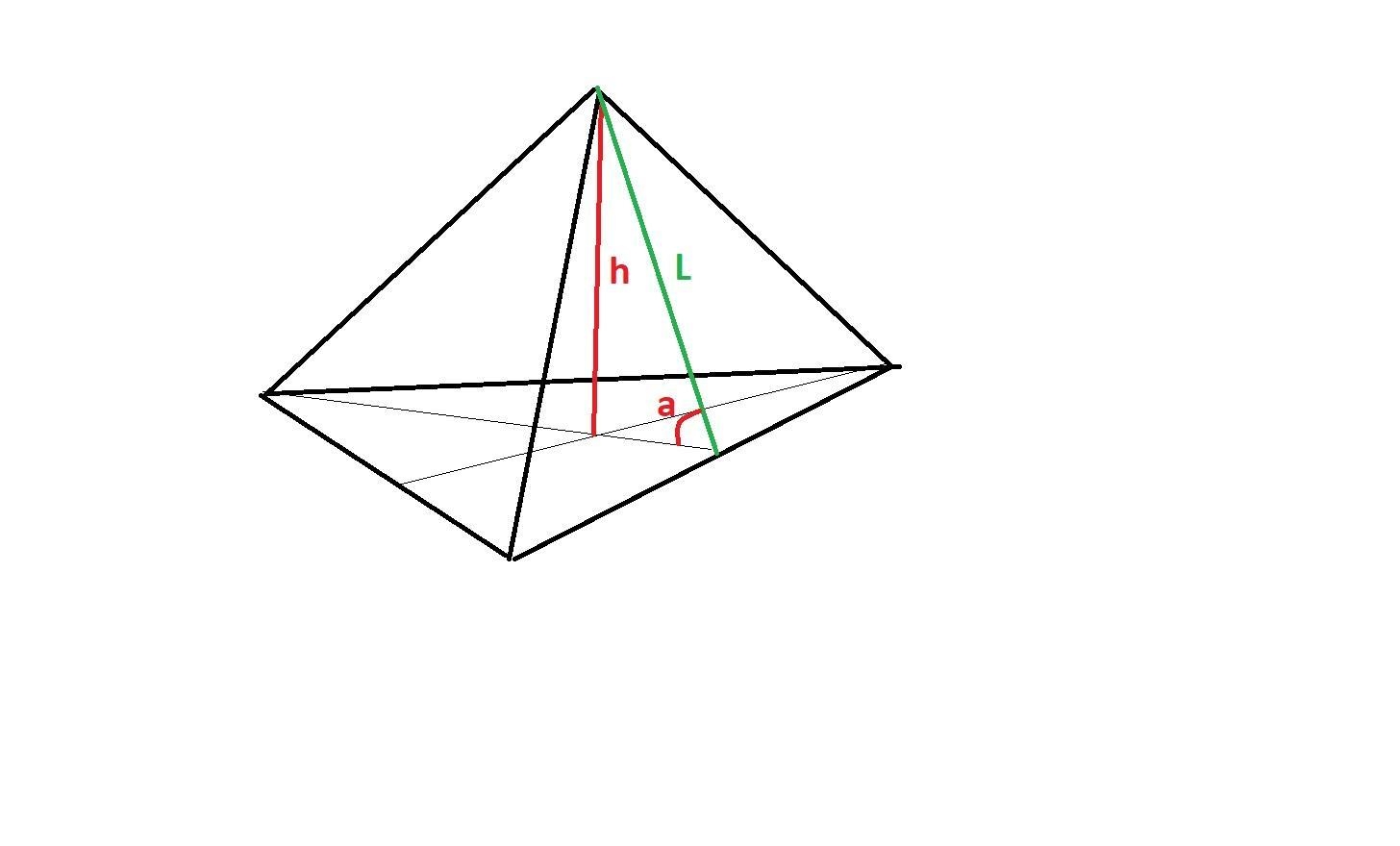
6

7
8

9

10

11
12
13

14
15

16

17
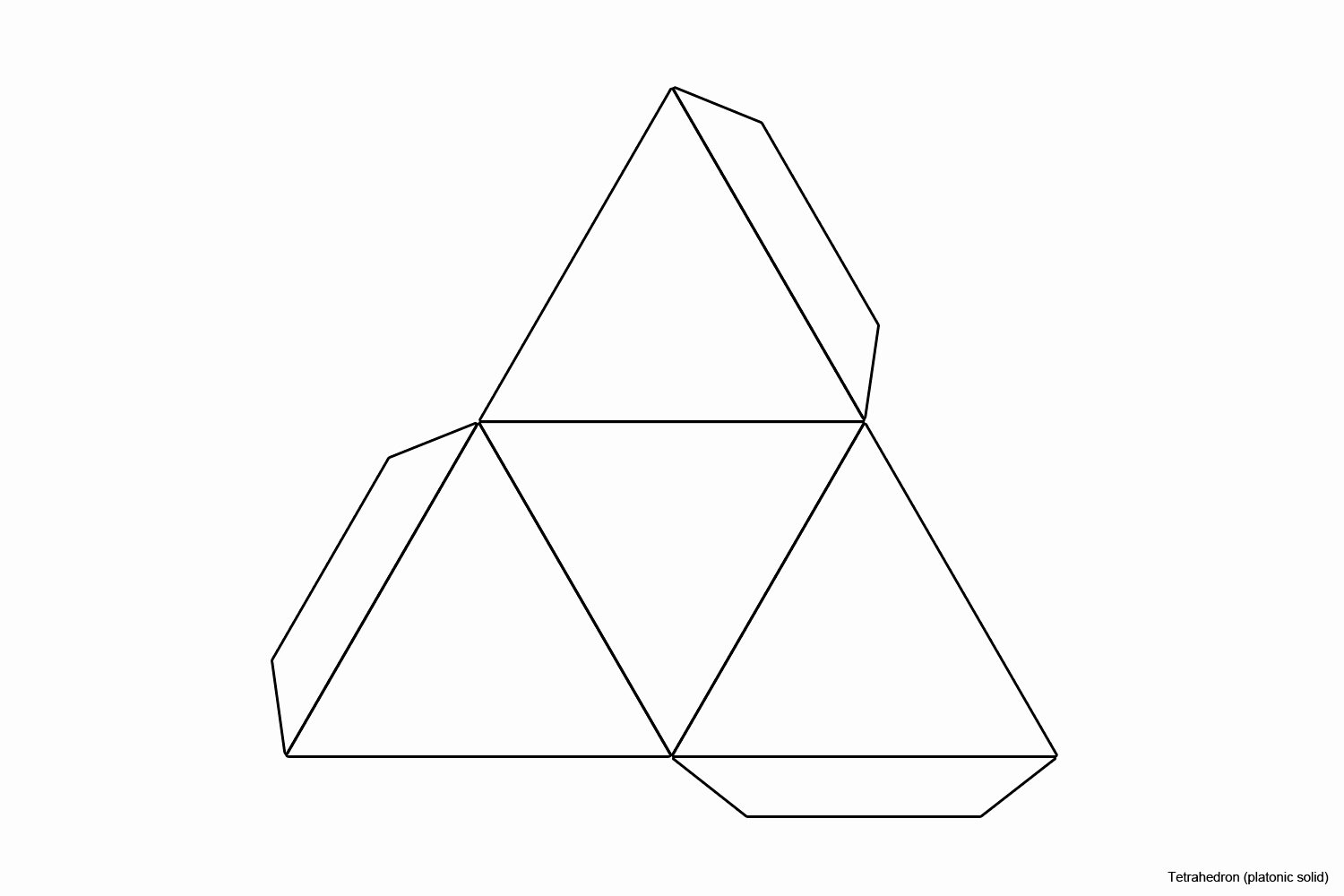
Усеченный треугольник

18
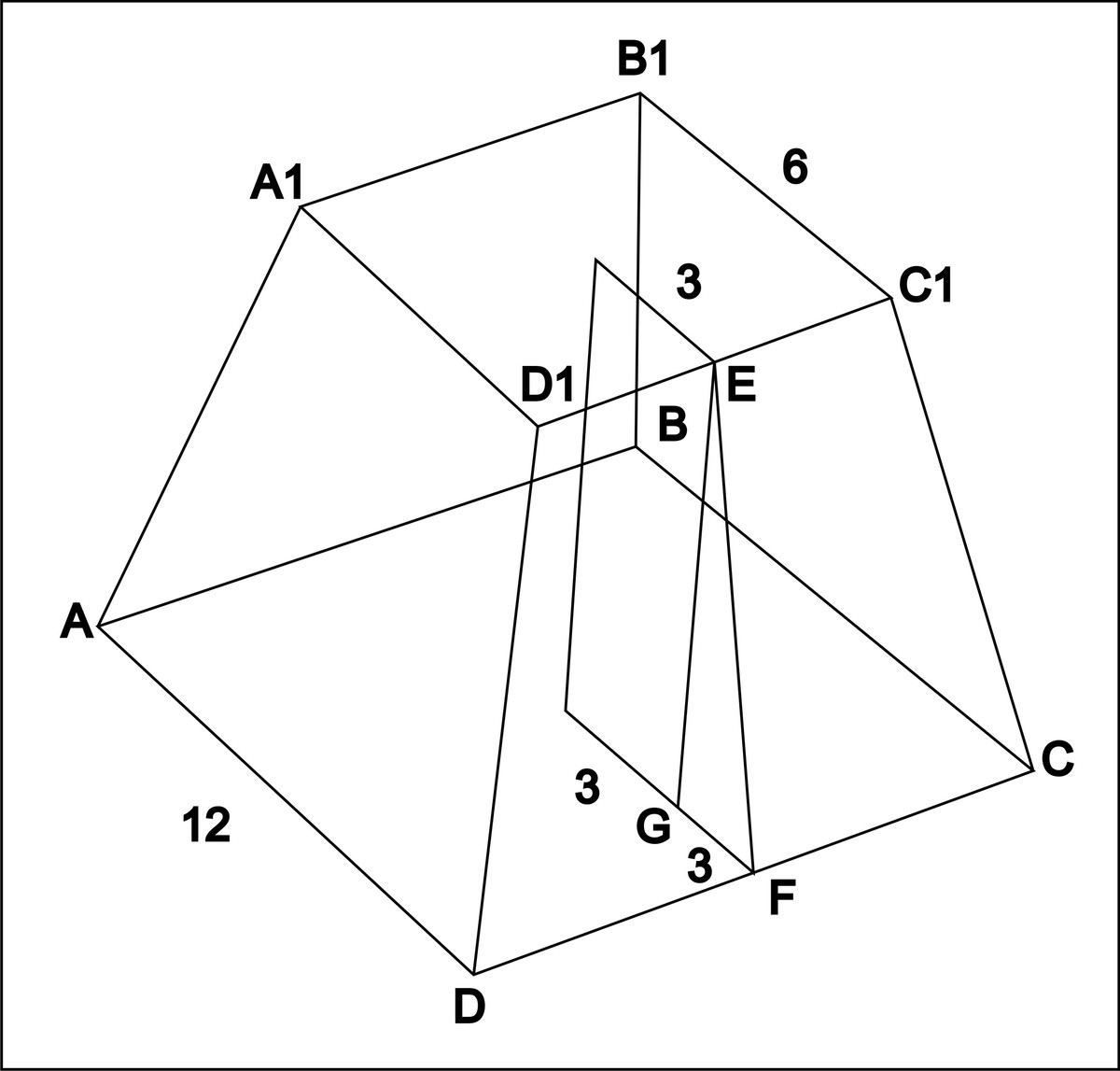
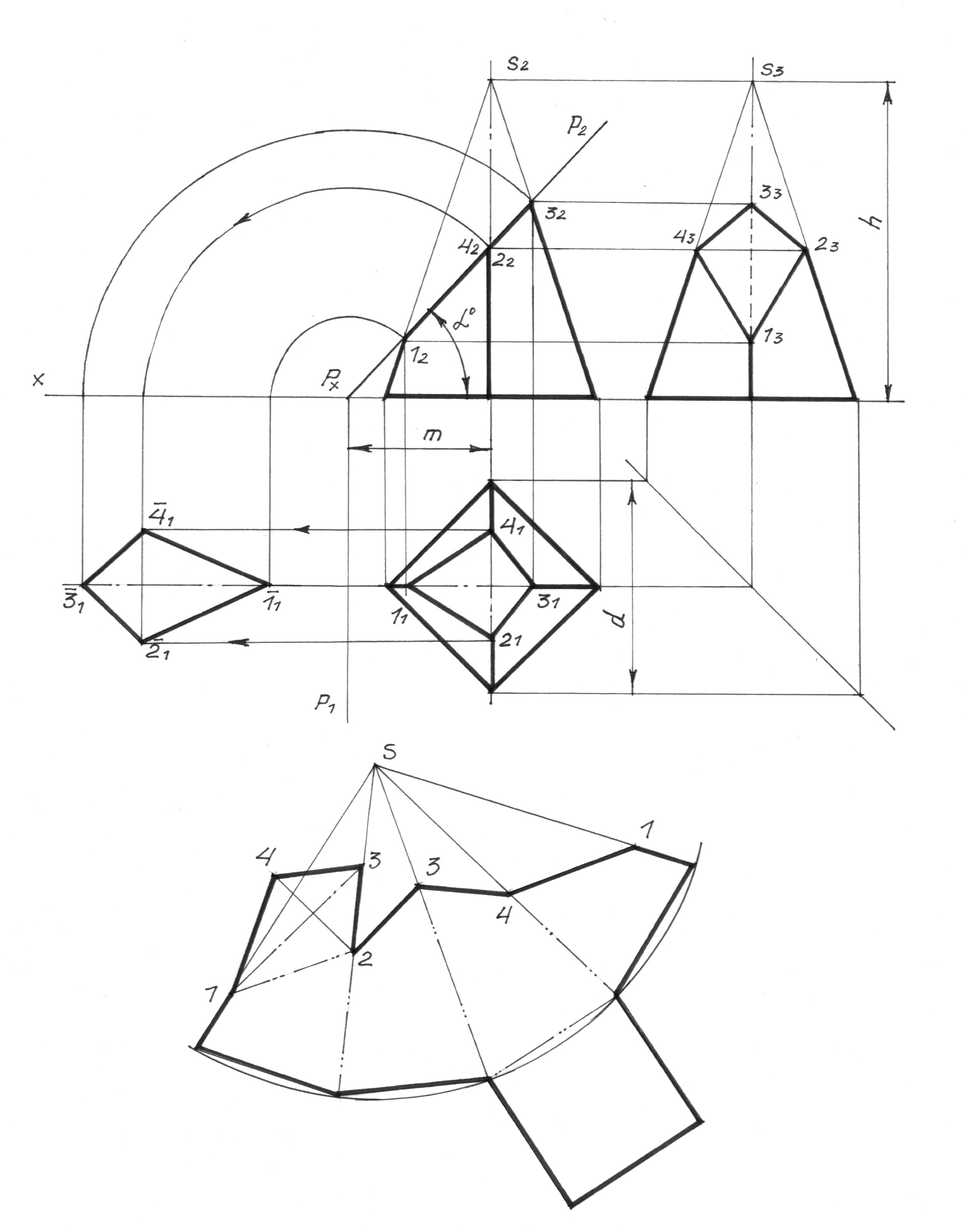
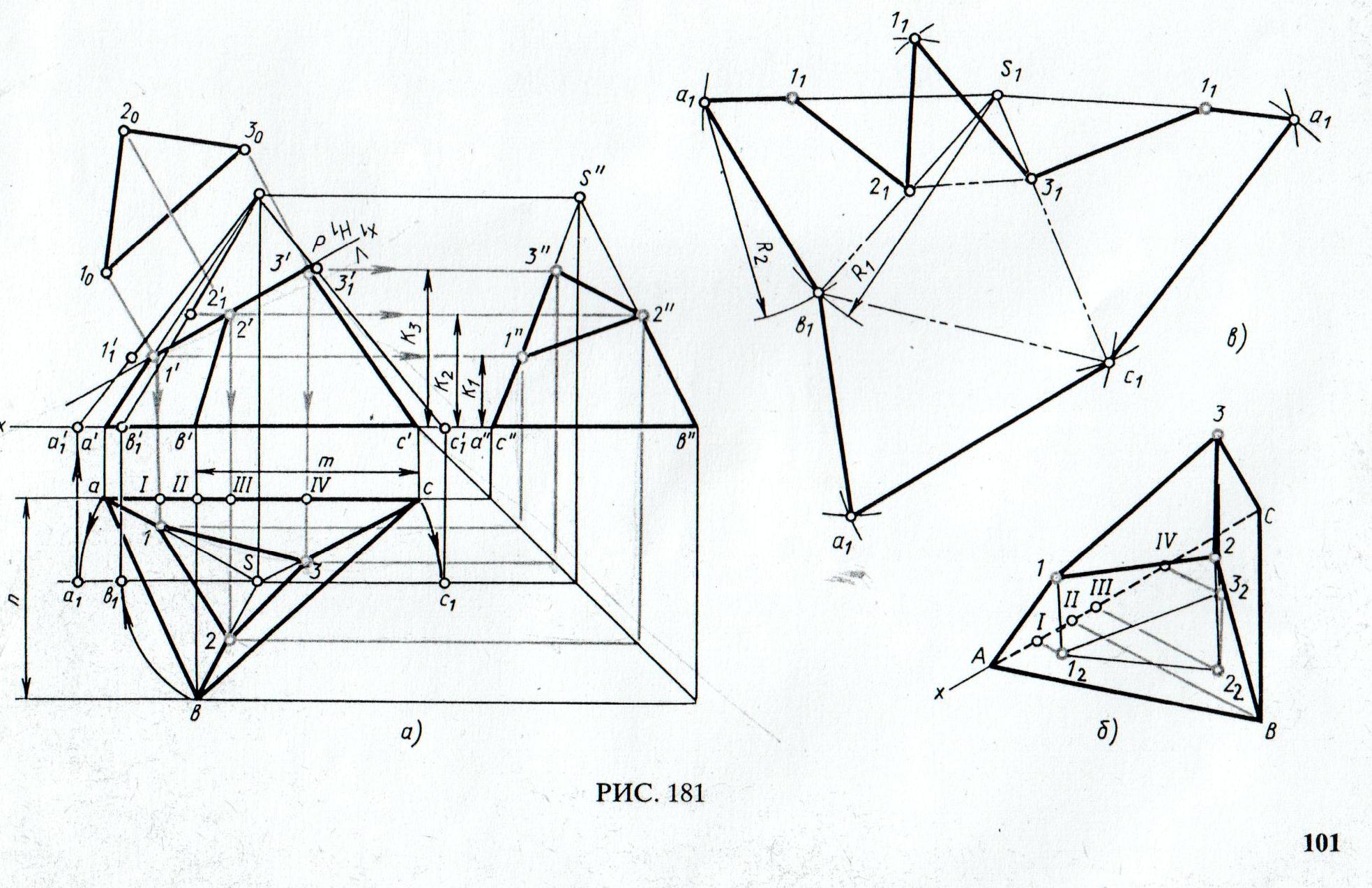
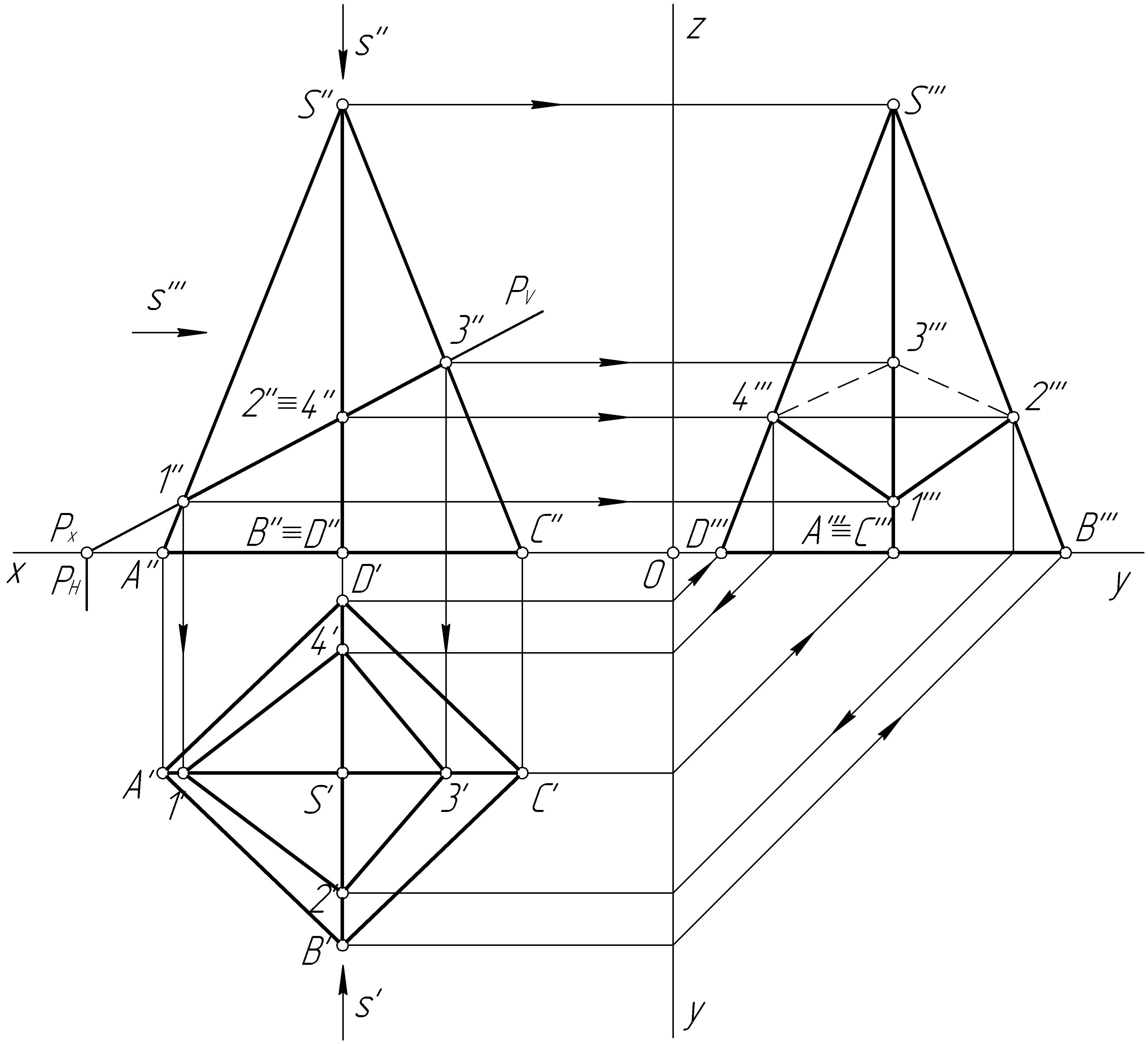
Проекции пирамиды со сквозным призматическим отверстием

19
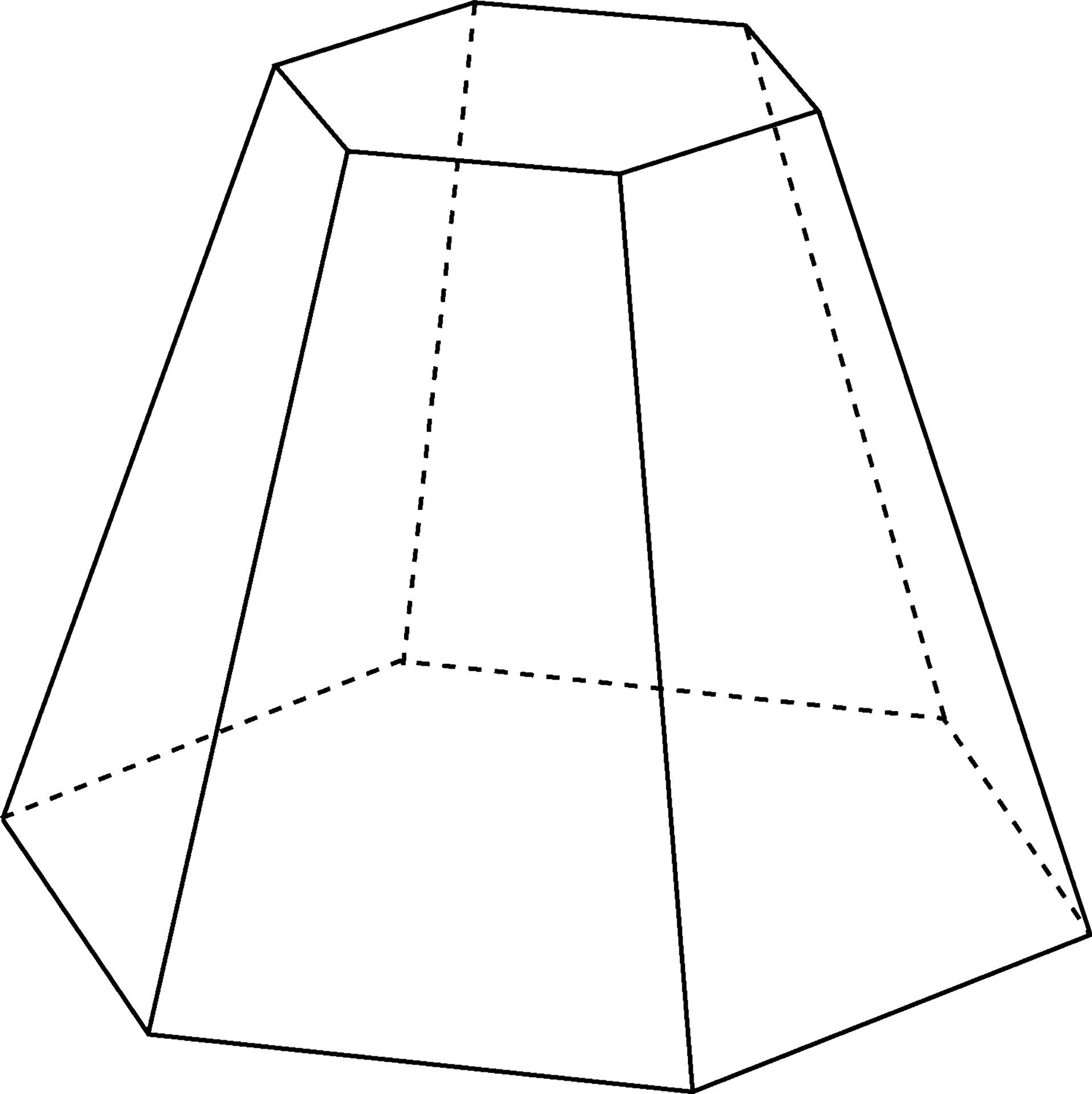
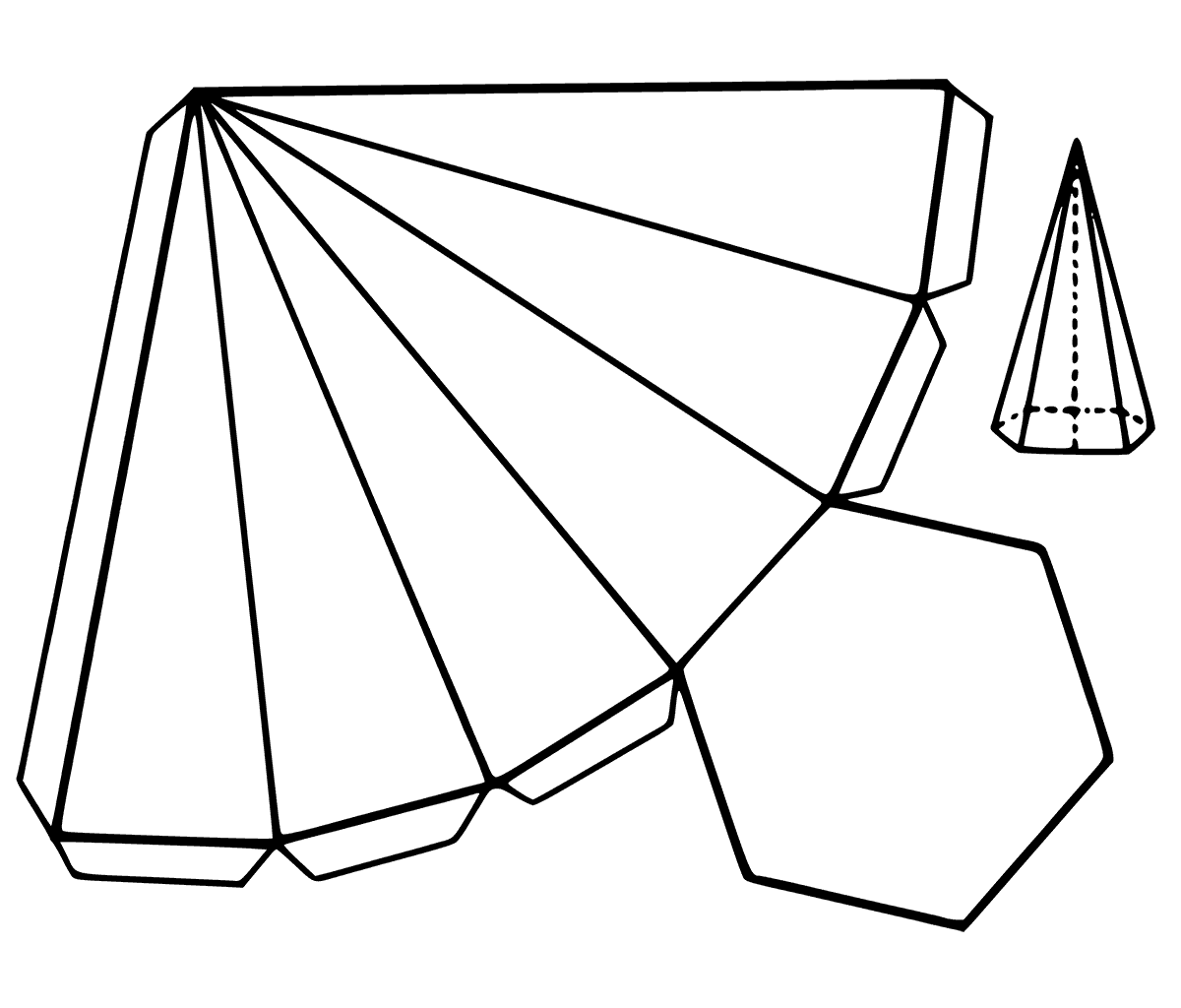
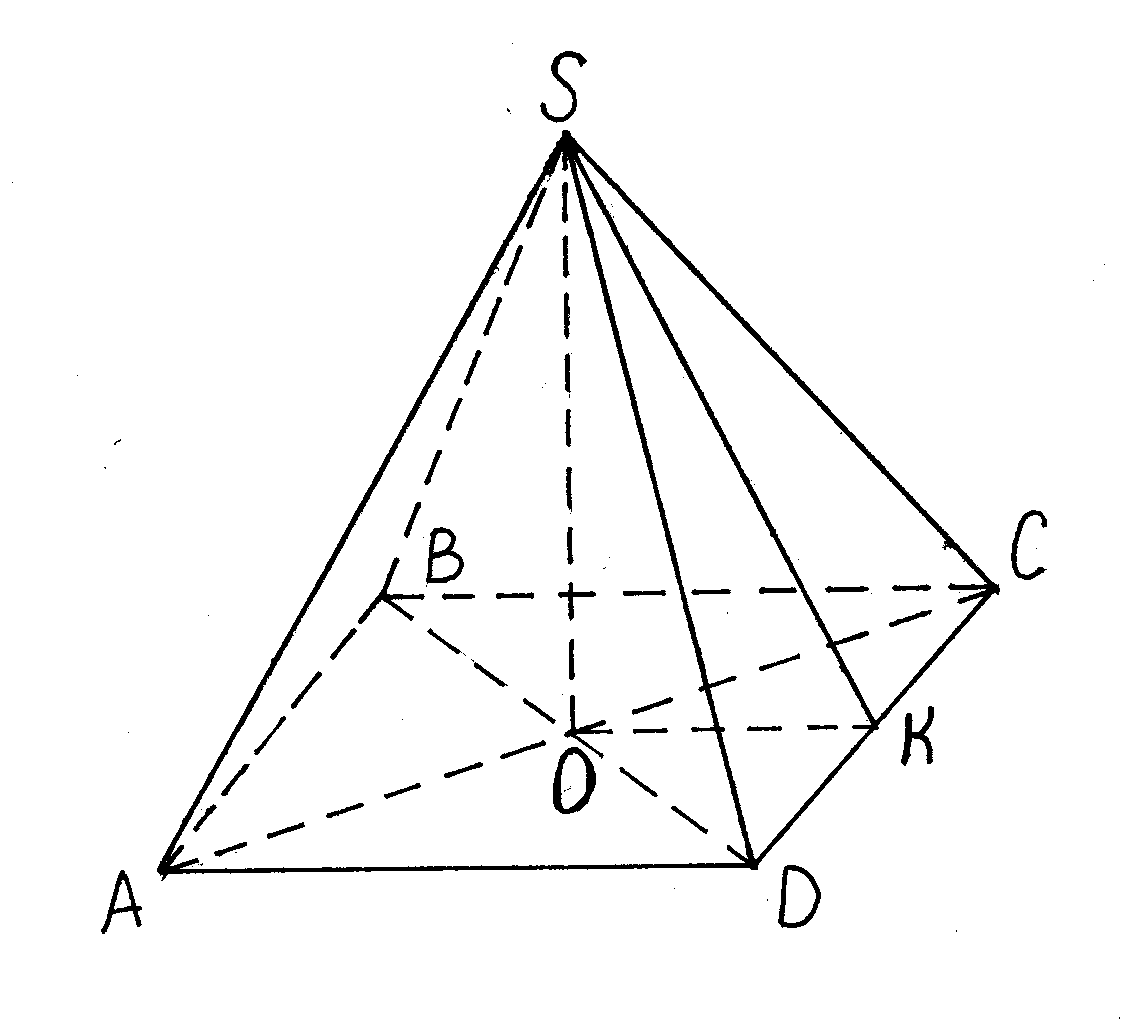
Пирамидка белая

20

21
22
23
24
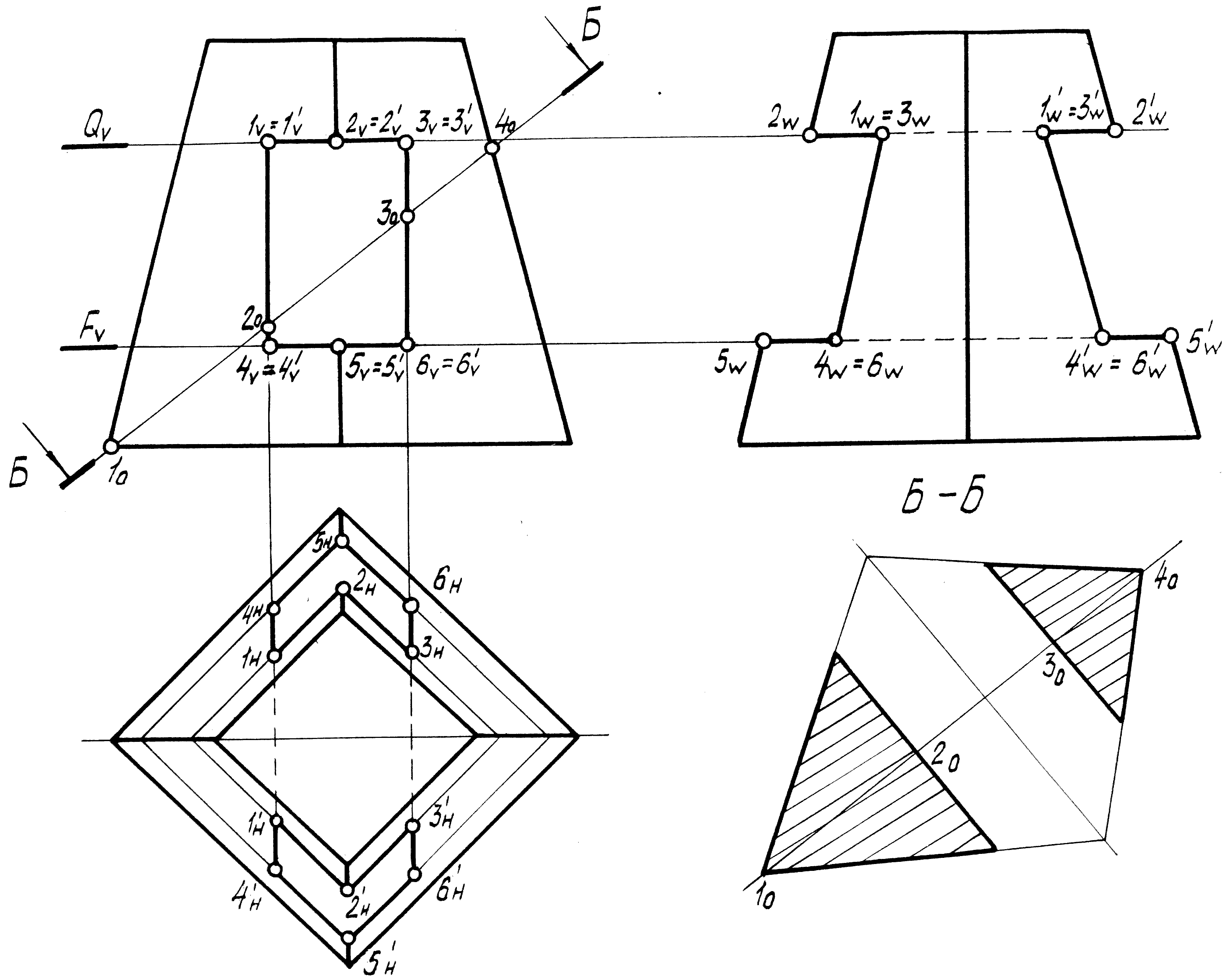
Ортогональный чертеж пирамиды

25
26

27
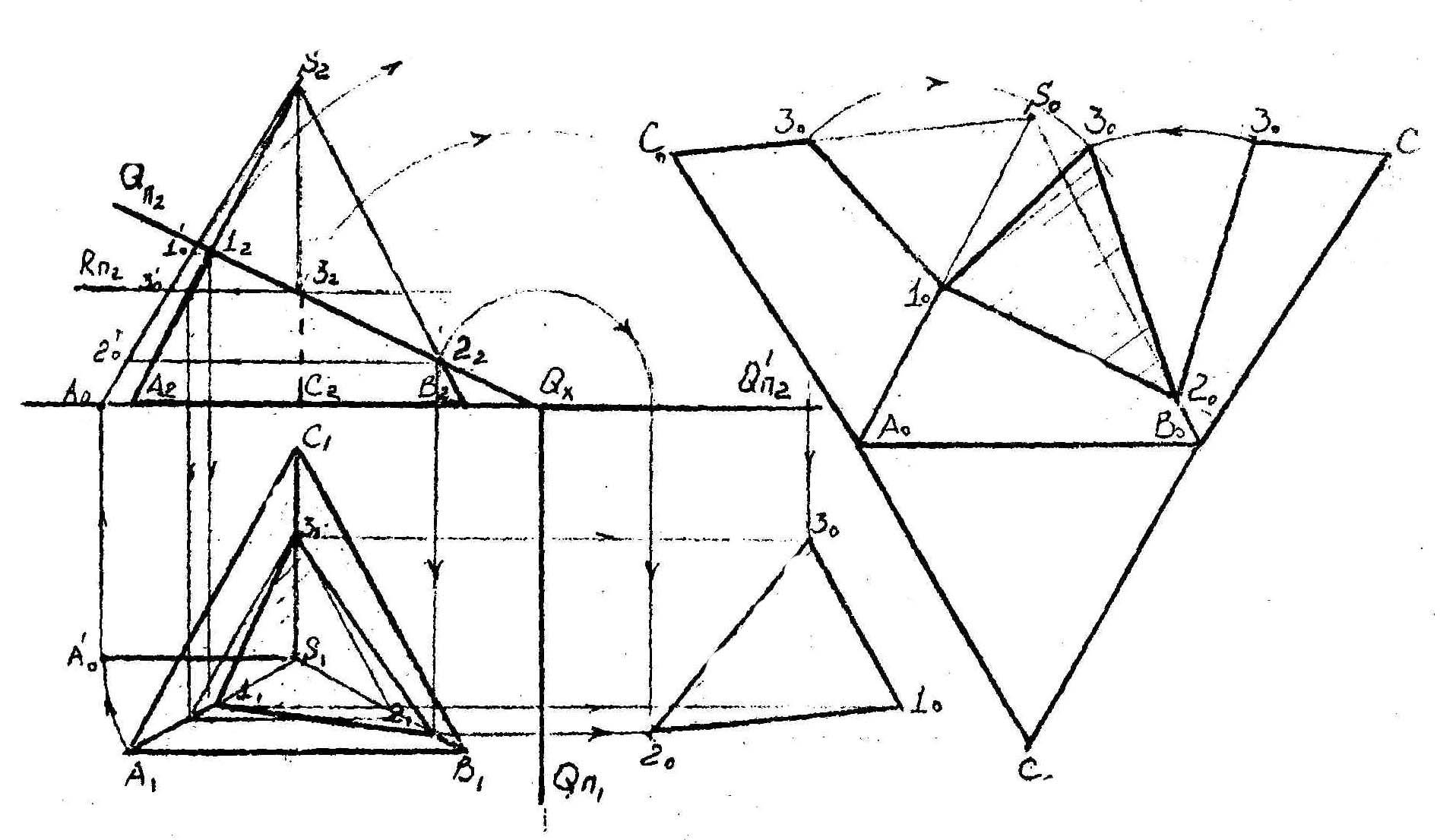
Сечение пирамиды плоскостью Инженерная Графика

28

29

30
31

32

33

34

35
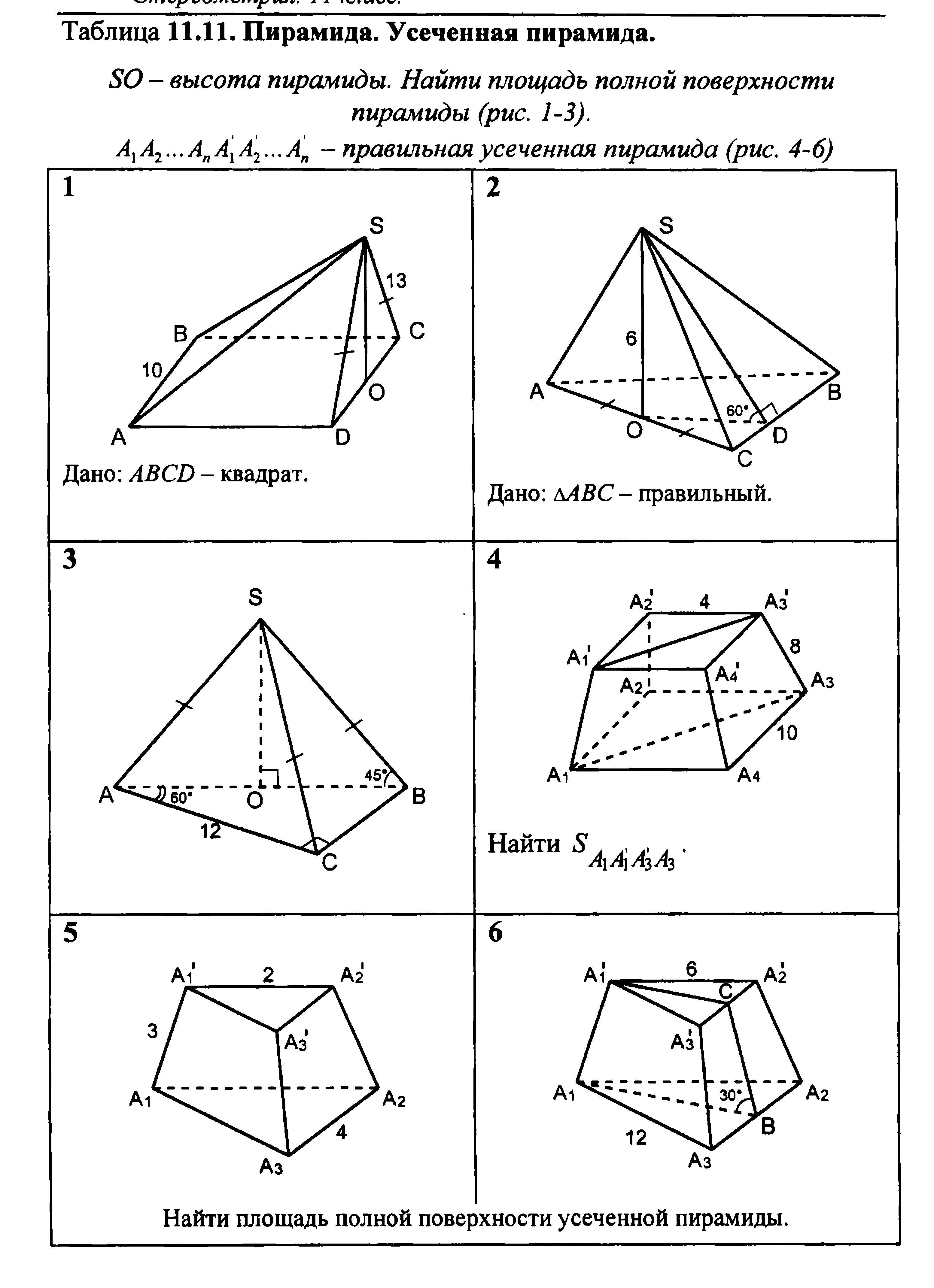
Стороны оснований правильной треугольной усеченной пирамиды равны 4

36

37
38
39
Апофема правильной четырехугольной пирамиды равна 2а

40
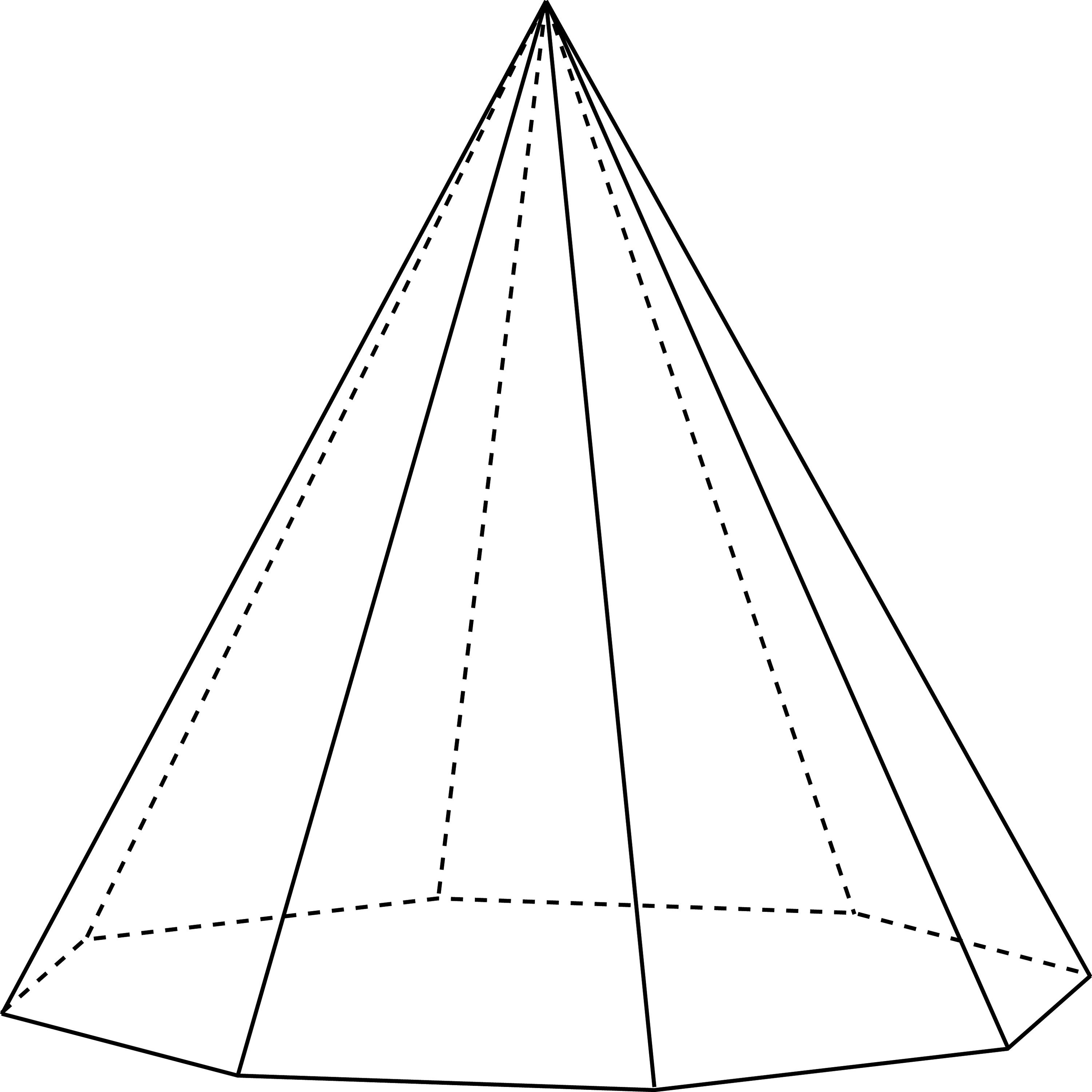
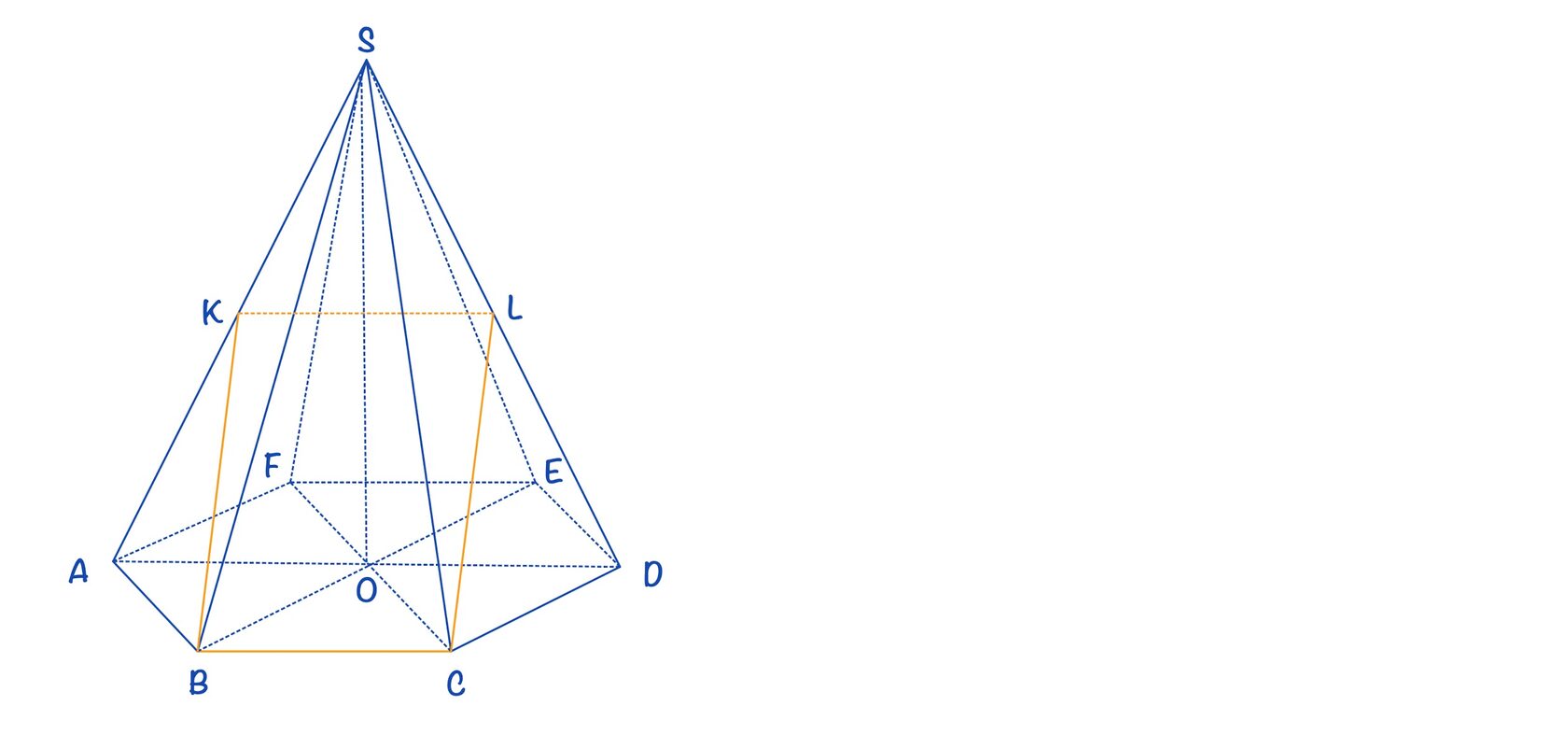
Апофема правильной шестиугольной пирамиды
41
42

43

44

45

46

47
Как найти апофему правильной треугольной усеченной пирамиды

48
49
50
51

52
Усеченная шестигранная Призма

53
Начертательная геометрия Призма

54
Стороны оснований правильной треугольной усеченной пирамиды равны 4

55
Сечение четырехугольной пирамиды чертеж

56

57
58
59
Пересечение пирамиды проецирующей плоскостью

60

61
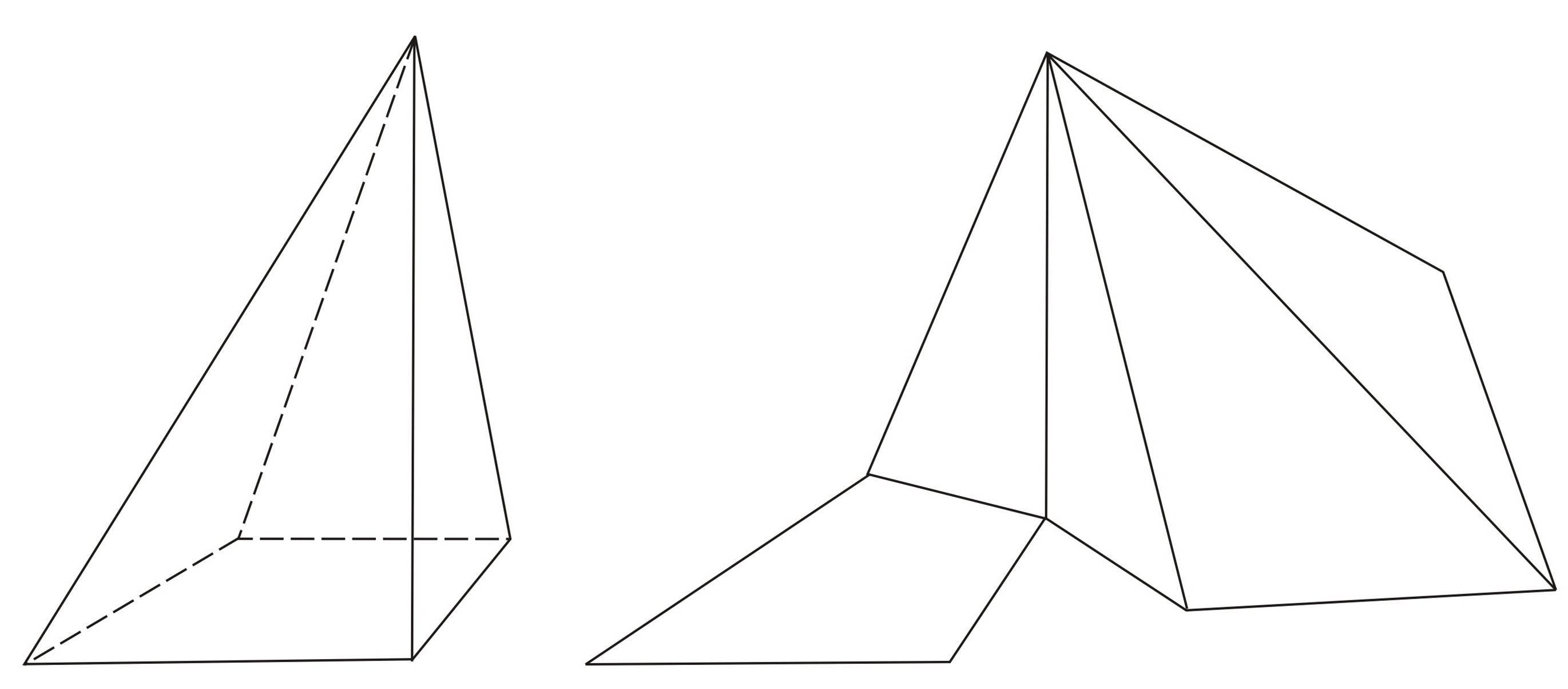
Развертка треугольной пирамиды Начертательная геометрия

62

63
Боковое ребро наклонено к плоскости основания под углом 45

64
65
Сечение пирамиды Начертательная геометрия

66
67

68
Стороны оснований правильной четырёхугольной пирамиды равны 6 и 8

69
Стороны оснований правильной четырехугольной усеченной пирамиды

70
71

72

73

74
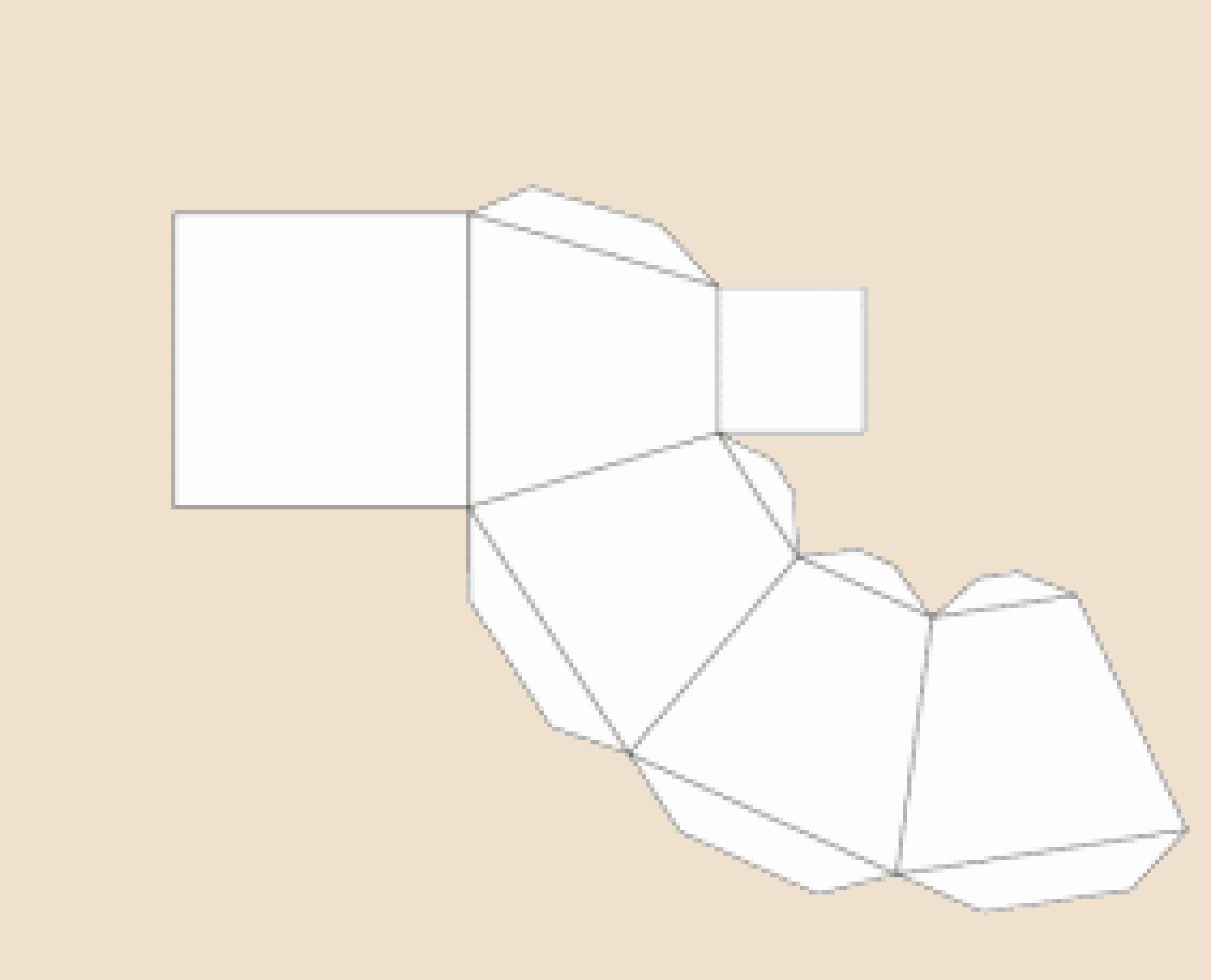
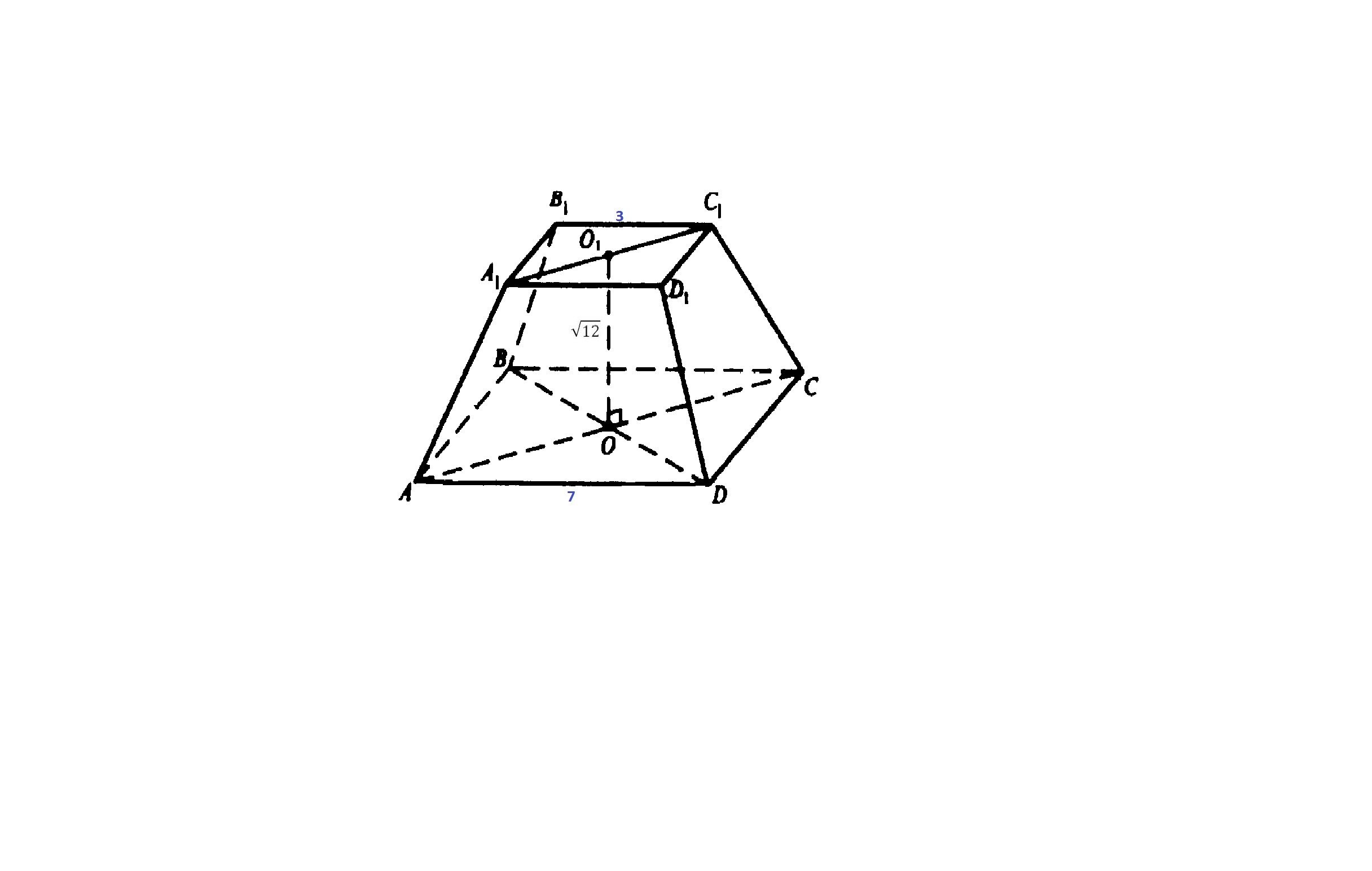
Развертка усеченной пирамиды черчение
75
76

77
78
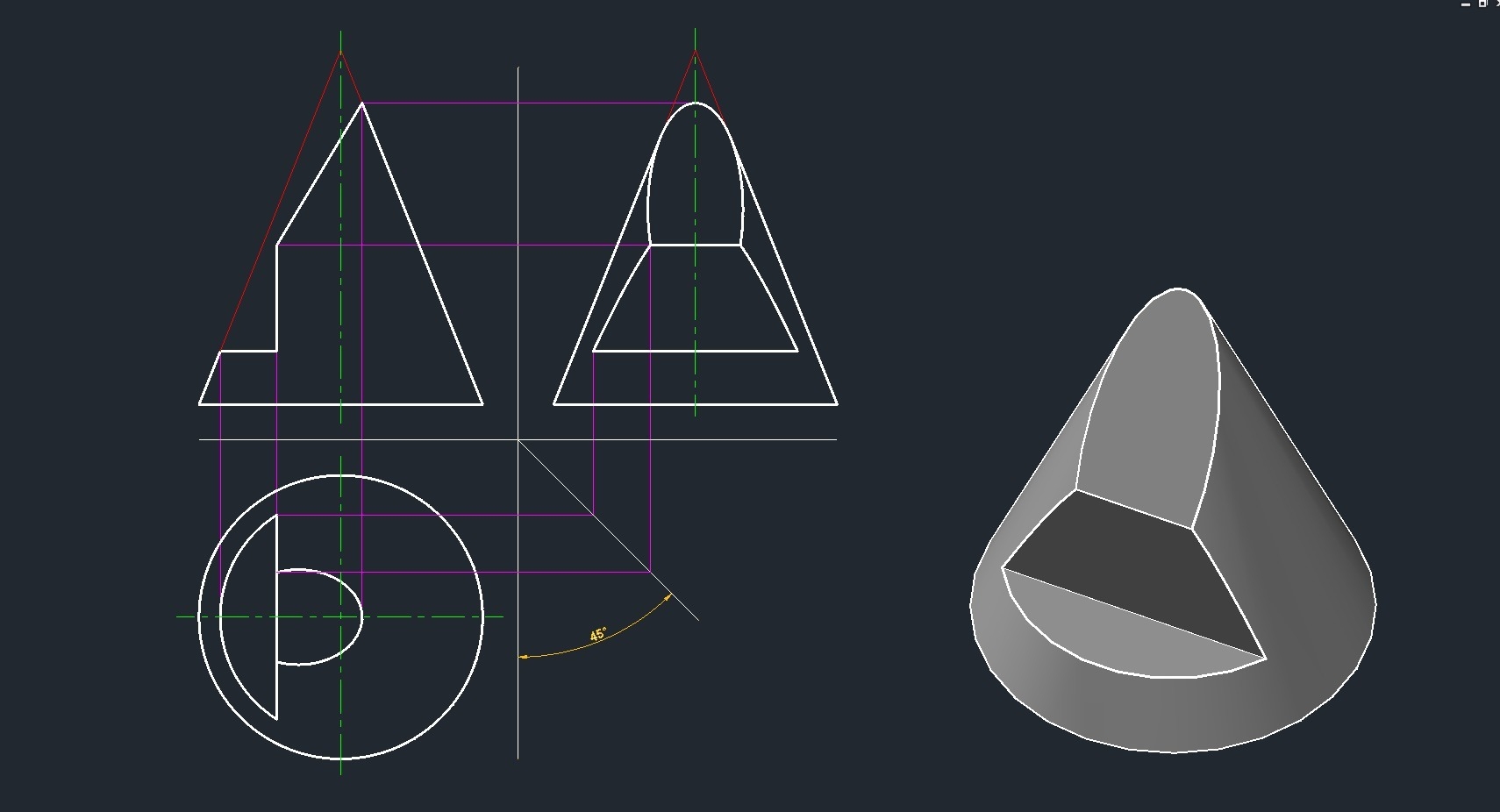
Начертательная геометрия проекция конуса
Свойства треугольной усеченной пирамиды
Треугольная усеченная пирамида обладает рядом уникальных свойств, которые делают её важным объектом для изучения в математике и геометрии. Её форма, объем, высота и боковая площадь - все эти параметры имеют свои особенности, которые можно исследовать и изучать.